April 20, 2023 : Wondercab Mini (40A)

TILES IN MOTION

There’s a video loop that’s been on my mind a good deal the last few weeks that I’d have loved to have been able to slot into the Cabinet right here right now, but it turns out you can’t always get what you want (who knew?). It came at the tail end of piece that ran in the New York Times a few weeks back (on March 28)

—Siobhan Roberts’s terrific report on an improbable breakthrough in the mathematics of tiling, the entirety of which you can access here, and indeed there, nestled at the very end of the piece, you will access the infinitely tumbling loop in question.

I won’t go into the history of the tiling problem here—Roberts does her typically clear, concise, and beguiling job in the article in question, well supplemented by an equally captivating account offered by longtime friend of the Cabinet, Margaret Wertheim, in a recent issue of her new substack Science Goddess, which you can find here. I love it that when it came to a breakthrough that had eluded the likes of the eminent Nobel laureate Roger Penrose (Stephen Hawking’s mentor!), who’d gotten stuck several years back one step shy of this ultimate solution, the fellow who turned out to make the decisive leap proved to be a modest, self-effacing cypher and complete nonprofessional outsider by the (near-perfectly anonymous) name of David Smith, who’d then had to seek out a small band of intrepid professionals to frame the discovery in terms a peer-reviewed journal would countenance (at first none of them could quite believe the development either). But that’s how it sometimes (even if almost never) happens. So do yourselves a favor and bone up on the particulars of this magical discovery on your own.

But I just want to return to that infinitely tumbling video (do you still have it unspooling there at the bottom of the NYT article from before, otherwise bring it back up here), because, as I say, I just can’t stop thinking about it. I find it completely mesmerizing (it’s a good thing it’s not offered as a screensaver, at least to my knowledge—and if I’m wrong, please don’t tell me—because if it were, I’d never get anything done). The way the field keeps oscillating, with maddening bouts of ever-tightening complexity suddenly giving way to momentary transports of utterly unstoppered simplicity (talk about a pillow of air!), before tumbling right back into all that confounding complexity all over again.

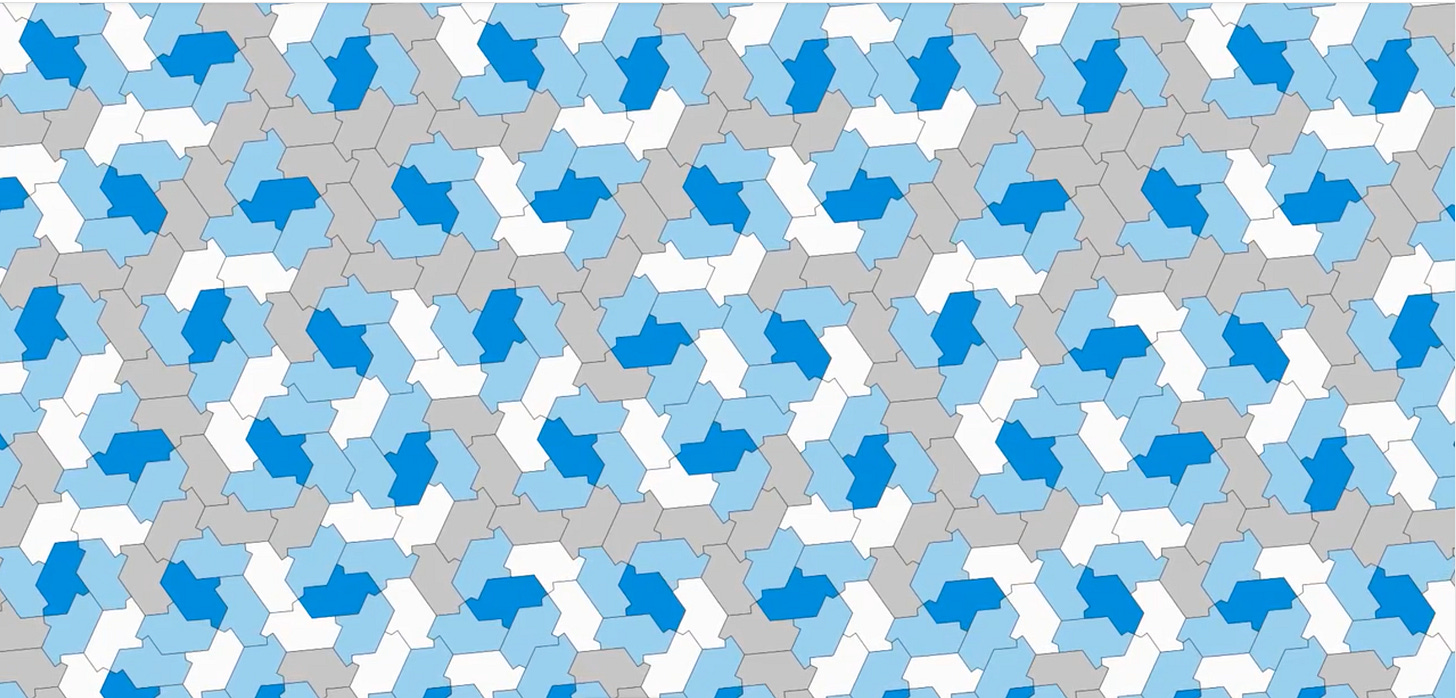
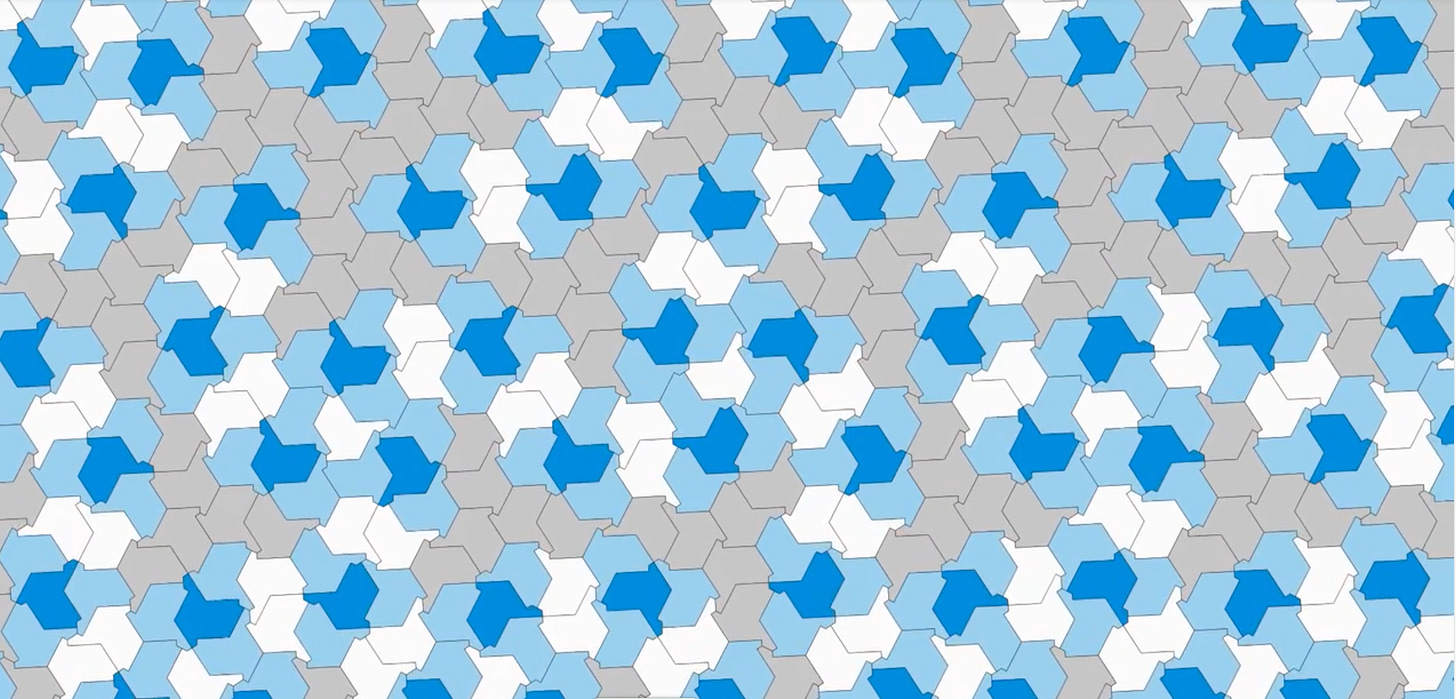
Start, for example, at the moment when the field is covered over with the very shape that David Smith himself discovered (uncovered? contrived?), the one he called a “hat” (specifically a kind of “rumpled fedora,” though I prefer to think of as a sort of tee-shirt), the one spread out across frame AA below (and note how in every frame, the entire expanse gets covered over with momentary polygons of exactly the same shape and size, though always in a non-repeating “aperiodic” as opposed to regular, “periodically repeating” array, the sort of thing you might see with the field of square or hexagonal tiles in your bathroom).

AA.

The shape keeps evolving, through all manner of further ungainly gerrymandered complexities until suddenly it opens out onto the airy simplicity of a field of chevrons (A) which is already giving way to renewed complexities (B) which eventually open out onto another field of airy simplicity (C) though it’s different from the previous one, being made up this time of apostrophe-like shapes (note incidentally that these shapes are miniature versions of the sort of thing that appeared throughout frame A, where two chevrons abutted in a particular way, especially visible in the white configurations).

A.

B.

C.

But here, too, the airiness quickly gives way as the tumbling reverses field and gives way to further succession of clotted gerrymandered complexities (D & E—and note how somewhere in here it sluices once more through a field of the David Smith hats/tee-shirts with which we began) before once more arriving (F) at the airy open field of chevrons and, reversing field once again, clotting back up into gerrymandered complexity (G). And so forth.

D.

E.

F (A).

G.

How does something that complicated become that simple, just like that, and then all complicated again? The whole process reminds me of a breakthrough materials scientists made a few years back. They were working on the holy grail of superconductivity, which is to say looking for a material that would conduct one hundred percent of an electrical pulse coursing through it (instead of shedding considerable percentages along the way in the form of heat, as happens with most conventional cables and wires, etc.), and they kept fiddling with materials that were evincing less and less shedding but then hitting a wall, they didn’t seem to be able to go any further. The breakthrough came, counterintuitively, when instead they began investigating super-insulators, materials that didn’t let any electricity through, and it turned out that in some cases the slightest tweaking of the lattices of those materials turned them into superconductors. (“By stacking two layers of graphene and then twisting them to precisely 1.06 degrees off-kilter, the material became insulating – until a certain voltage was applied, at which point it suddenly switched to become superconductive.” For more on which see, for example, here.)

From utter blockage to absolute flow!

Or, for another example, consider the behavior of pendulum arrays, as for example, in this video, here:

From hapless chaos to serene order, and back out again.

Which is to say, just like life. Or the life of the writer at any rate. Nothing seems to be working and nothing seems to be working, and then suddenly (momentarily) the lattice opens wide and you can do no wrong. And then it closes down again.

NOTE: Special thanks this week to Professor Craig Kaplan at the University of Waterloo in Canada, the creator of that marvelous video graphic of the tumbling polygons at the end of the NY Times article, for his help in explaining it to us.

* * *

ONE LAST THING BEFORE WE TAKE OUR LEAVE…

With this issue, we complete the fortieth of our fortnightly exertions, which seems like a good moment to take stock of how we are doing. And some of the news is good: our increase in total subscribers continues from week to week (we are now approaching 3,700 total)—with a steadily high rate of "subscriber engagement" (readers who open each issue, or at least a lot of them)—and so does our total population of paid subscribers (we are approaching 170). But frankly, this is still way too small a base from which to make this project a sustainable proposition long-term. (Moment of candor born of alarm: Ren tabulates that he has been compiling the Cabinet, across the entire length of its run, for what turns out to be an average of $75 a week. To which David says, “Yikes! Maybe you should consider babysitting instead.”)

And yet we remain irrevocably committed to not instituting any sort of paywall, keeping everything open to everyone. That being at the very heart of the entire enterprise: Mirabilia Omnibus! (Wonder for All!)

So our mission needs to be to generate enough subscriber support that we can afford to do the work. We hope these first 40 issues have given you confidence in our commitment to quality.  

We are deeply appreciative of those who have chosen to become paid subscribers and hope that in the weeks and months to come more of you will choose to join them. (We know that not all readers can.) Of late, a few very generous patrons have stepped in to help us at levels over and beyond the conventional, and we are especially grateful to them. You all give us hope for the future. 

Even if you can’t afford a financial commitment, though, what would really help would be the simple act of sharing word of our existence with a few of your friends, by hitting the SHARE button below. The faster we increase our total subscriber base, the greater will grow the number of those who can and do choose to pay. 

We're hoping the whole process of building support is a little like the tiling video -- blockage and blockage, complication upon complication, but then suddenly, the field opens up and all is airy flow. Maybe, with the coming of springtime, this week will even be that week! Please give it a thought. 

Okay: enough!  

We'll see you next week, and the one after, and the one after that, for as long as we can.  

Thank you for giving Wondercabinet some of your reading time! We welcome not only your public comments (button below), but also any feedback you may care to send us directly: weschlerswondercabinet@gmail.com.

Here’s a shortcut to the Complete Wondercabinet Archive.